Cubic-to-Trigonal Transition
Introduction
The cubic-to-trigonal transition is described by two parameters,
a trigonal angle 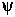 and a
stretch. The trigonal angle is the angle between two intersecting
edges of the parallelepiped forming a trigonal unit cell; while,
the stretch is proportional to the ratio of the length of a side
of the cubic unit cell and the length of a side of the trigonal
unit cell. The trigonal angle is, however, the fundamental parameter
describing the transformation, because for all alloys considered,
the stretch is nearly unity.
and a
stretch. The trigonal angle is the angle between two intersecting
edges of the parallelepiped forming a trigonal unit cell; while,
the stretch is proportional to the ratio of the length of a side
of the cubic unit cell and the length of a side of the trigonal
unit cell. The trigonal angle is, however, the fundamental parameter
describing the transformation, because for all alloys considered,
the stretch is nearly unity.
Some alloys undergoing this transition are
- Au-Cd, Terfenol (Tb-Dy-Fe), Ti-Ni, Ti-Ni-Al, Ti-Ni-Fe.
In Ti-Ni, this is the R-phase; R denotes rhombohedral which is equivalent
to trigonal.
There are several possible transitions between a cubic Bravais
lattice and a trigonal Bravais lattice:
- the transition between simple cubic and trigonal is evident,
and
- the transition from either body-centered cubic (BCC)
or face-centered cubic (FCC) to trigonal follows from the well-known
fact that each of these cubic lattices contains a trigonal unit cell.
Figure 1 shows a cubic unit cell and a trigonal unit cell along with
the trigonal angle 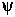 .
.
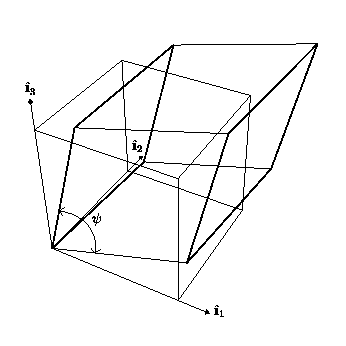
Figure 1: Trigonal unit cell (dark thick lines) and a
cubic unit cell.
Notice, that for trigonal angles less than 90 degrees, the
transformation can be achieved by an expansion along the body
diagonal [111] of the cube; while, for trigonal angles greater
than 90 degrees, it is a contraction along the body diagonal
[111] of the cube which gives a trigonal unit cell.
Transformation Stretch Matrices
The transformation stretch matrices are the gradient of the
deformations which take a cubic lattice into a trigonal lattice.
There are 4 such matrices, one for each variant of the martensite
phase. They have components
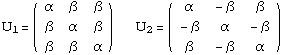
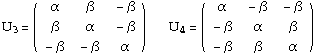
The components 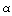 and
and
 are functions of the
trigonal angle
are functions of the
trigonal angle 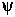 .
Specific details can be found in reference [1].
Also, James and Kinderlehrer [2] have studied
some microstructures in this transition during their study of
magnetostriction in Terfenol.
.
Specific details can be found in reference [1].
Also, James and Kinderlehrer [2] have studied
some microstructures in this transition during their study of
magnetostriction in Terfenol.
Microstructures for the Cubic-to-Trigonal Transition
Here are links to various pages, where a number of different
microstructures are discussed. Also contained therein is a
table showing the possible microstructures for the
cubic-to-trigonal transition.
References
-
``Microstructure in the cubic
to trigonal transition.'' by Kevin F. Hane and Thomas W. Shield.
To be submitted to Materials Science and Engineering A, 1998.
-
``Theory of magnetostriction with
applications to Tbx Dy1-x Fe2.''
by Richard D. James and David Kinderlehrer, Philosophical
Magazine B 68, 237 (1993).
Top of this page.
Back to main page.
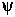 and a
stretch. The trigonal angle is the angle between two intersecting
edges of the parallelepiped forming a trigonal unit cell; while,
the stretch is proportional to the ratio of the length of a side
of the cubic unit cell and the length of a side of the trigonal
unit cell. The trigonal angle is, however, the fundamental parameter
describing the transformation, because for all alloys considered,
the stretch is nearly unity.
and a
stretch. The trigonal angle is the angle between two intersecting
edges of the parallelepiped forming a trigonal unit cell; while,
the stretch is proportional to the ratio of the length of a side
of the cubic unit cell and the length of a side of the trigonal
unit cell. The trigonal angle is, however, the fundamental parameter
describing the transformation, because for all alloys considered,
the stretch is nearly unity.

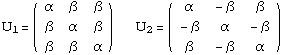
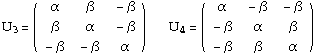
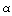 and
and
 are functions of the
trigonal angle
are functions of the
trigonal angle