Ryan S. Elliott ProfessorResearch Summary(see also the distinct research projects in my group) |
 |
Short Course on:
Stability and Bifurcation Theory and Its Systematic Application
This is an intensive 3–5 day short course appropriate for participants in the
engineering, science, or mathematics disciplines at the graduate, professional,
or university faculty level. For more information, see
the
course
flyer.
VIA ATOMIC LEVEL SIMULATION
Introduction: ``Intelligent'' or ``active'' materials possess the uncommon ability to significantly change their properties, such as their shape, hardness, or color, in response to an external stimulus. Current applications include medical devices such as vascular stents, orthodontic archwires, and shape changing surgical tools made from shape memory alloys; electronic ignition devices, inkjet printers, and accelerometers (like the ones used in Wii video game controlers) made from piezoelectric materials; and also digital data storage chips, made from ferroelectric materials, that could be used in devices like the iPhone and iPod. Future applications are likely to include ultra-efficient refrigeration devices made from magnetic shape memory alloys and ``energy harvesting'' devices that could, for instance, charge your cellphone while you walk by extracting electricity from the shock-absorbing deformations that occur in your shoes.
Shape Memory Alloys (SMAs) are a particular class of intelligent materials with the amazing ability to crumple, bend, and generally undergo large deformations in response to an applied load and to immediately recover their initial shape when the load is removed (an effect called ``pseudoelasticity''). Additionally, cold SMAs will remain crumpled after removal of the load and will only recover their initial shape once the temperature has been increased (the ``shape memory effect''). For example, a hot spoon, made of the SMA NiTi (an alloy composed of half Ni atoms and half Ti atoms), bent into a U shape will immediately straighten; however, if the spoon is cold it will stay in the U shape until it is heated. Because of these remarkable abilities, the use of SMAs in medical devices and instruments is a rapidly growing multi-billion dollar industry. Innovation in this area is currently centered in Minnesota at companies like Medtronic and Boston Scientific.
Clearly, SMAs and other intelligent materials have the potential to dramatically transform all areas of human activity. However, for this transformation to be realized new and improved active materials must be developed. A key barrier to this development, and the focus of my research program, is the lack of accurate and efficient atomic level simulation techniques for the design of intelligent materials.
 Background: Materials simulation techniques such as
Elasticity Theory and Plasticity
Theory are used to predict the behavior of engineering
materials such as steel, aluminum, and titanium. These theories are based on a
set of rules that describe the bulk (macroscopic) behavior of a material. By
using these rules and a small set of experimental data it is possible to
accurately predict the material's bulk behavior in a wide range of situations.
Unfortunately, no appropriate set of bulk behavior rules is known for active
materials. This is because of the intricate patterns and complex phenomena
exhibited by these materials at the micro and nanoscale which transcend scales
and affect macroscopic behavior. Thus, the development of bulk behavior rules
for active materials requires one to study how the atoms comprising the
material interact.
Background: Materials simulation techniques such as
Elasticity Theory and Plasticity
Theory are used to predict the behavior of engineering
materials such as steel, aluminum, and titanium. These theories are based on a
set of rules that describe the bulk (macroscopic) behavior of a material. By
using these rules and a small set of experimental data it is possible to
accurately predict the material's bulk behavior in a wide range of situations.
Unfortunately, no appropriate set of bulk behavior rules is known for active
materials. This is because of the intricate patterns and complex phenomena
exhibited by these materials at the micro and nanoscale which transcend scales
and affect macroscopic behavior. Thus, the development of bulk behavior rules
for active materials requires one to study how the atoms comprising the
material interact.
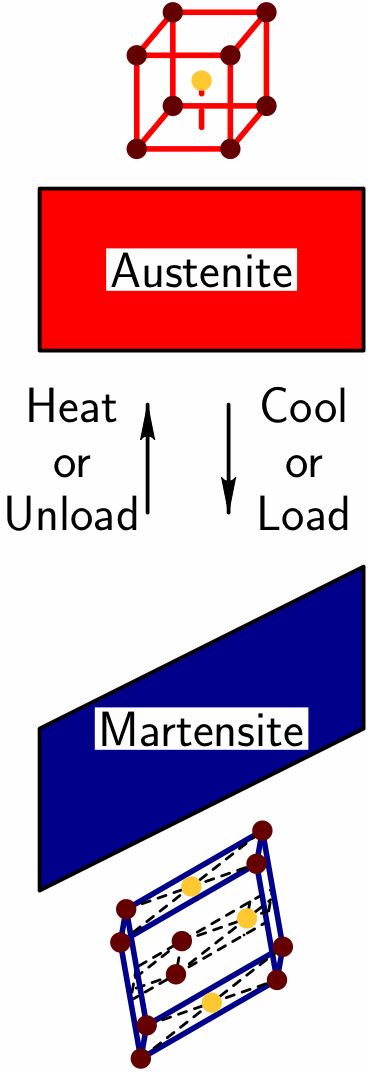
SMAs serve as an excellent prototypical class of intelligent materials. It is known that their remarkable properties derive from a reversible ``martensitic phase transformation.'' As schematically illustrated here, above a critical ``transformation temperature'' the atoms in these crystalline materials like to arrange in a high symmetry shape (eg., a cubic arrangement), called the ``austenite phase.'' For lower temperatures, the atoms prefer a lower symmetry shape (eg., a prismatic arrangement), called the ``martensite phase.'' Thus, as the material is cooled to the critical temperature the austenite phase becomes ``unstable'' and the atoms rearrange in a coordinated fashion so as to transition to the martensite phase. The result is an overall change in shape that can move a desired object. This same martensitic transition occurs when a mechanical load is applied.
The key to understanding why only special materials exhibit SMA behavior lies in simulation at the atomic level. Current simulation techniques rely on random or ad hoc searches for the austenite and martensite phases. Due to the vast number of phases that must be considered (eg., all possible shapes that can be obtained by deforming a cube), progress in the field has been slow. The challenge, then, is to develop new atomic level simulations that can systematically identify a small set of relevant phases to be searched and thereby enable the discovery of new intelligent materials.
The development of one such technique has been the major contribution of my research to date. As temperature is decreased the austenite phase initially responds by contracting slightly. This can be represented as a ``path'' or ``branch'' through the set of all possible phases of the material. My atomic level simulation technique starts by following this branch. When the transformation temperature is reached the path forks or ``bifurcates.'' The material then ``turns'' onto the new branch which leads to the martensite phase. By characterizing these branches and their forks the technique creates a map of all branches the material can travel along. Of particular importance is the technique I developed to identify not only the stable parts of these paths but also which stable phases will result in a reversible transformation. This information identifies the phases of the material that can be observed in experiments. The final maps represent a systematic investigation of all possible branches for a material and dramatically reduce the number of phases that need to be considered to predict SMA behavior. References to my publications in this area are provided on my curriculum-vitae.
Vision: The goal of my research program is to develop tools
that allow engineers to design, at the atomic level, the basic materials
that are used in the construction of a device or structure.
| Design of | Scale | Example | Simulation Technique | |
| ok | Structures | 102m – 10-2m | Skyscrapers use beams & plates. | design codes handbook |
| ok | Devices | 10-2m – 10-6m | iPhone uses 3D case & circuit boards. | 3D Finite Elements |
| X | Materials | 10-6m – 10-10m | A biocompatible SMA tuned to a specific individual's body chemistry. | atomic level simulation |
Currently, design tools are common at the structural and device scale but accurate and efficient materials design tools, especially intelligent material design tools, are not available. My vision is to develop such a set of tools for materials design using atoms as the basic design elements.
To achieve this vision, I have initiated an independent research program consisting of three related tasks, described below, that I believe will significantly contribute to our fundamental understanding of why intelligent materials exist and how we can use atomic level simulation to design new active materials.
New BFB simulation techniques for intelligent materials: In my Ph.D. dissertation I introduced a new ``Branch-Following and Bifurcation'' (BFB) atomic level simulation methodology based on empirical atomistic interactions and the mathematical theory of bifurcation and stability. Bifurcation and stability theory provides the tools for quantitatively mapping out the austenite and martensite phases of a material and for identifying the paths and connections between these phases. The detailed BFB map allows for a deep understanding of the material's behavior that can not be obtained from other common simulation methods. This methodology has proven its ability to accurately predict the existence of active material behavior and further, has the potential to discover entirely new intelligent materials!
However, for the BFB methodology to realize its potential a fundamentally new approach to simulate atomic interactions must be used. This will require the adoption of recent advances in accurately simulating atomic interactions, including the quantum-mechanics based ``Density Functional Theory'' (DFT) technique. Additionally, a new set of sophisticated algorithms must be developed that can systematically and automatically apply the tools of bifurcation and stability theory. These must be specialized, when possible, to take advantage of unique features of a particular problem such as symmetry or constraints. Work in these new research areas has already begun and I believe that, with sufficient resources, significant progress can be achieved by my group within the next few years. The project's ultimate goal is to develop a self-contained software package that is sufficiently sophisticated to solve the complex problem of intelligent material design and characterization while providing a simple user interface that is attractive to a wide class of users in both academia and industry.
Composition effects on the behavior and properties of active materials: Many material properties are known to exhibit extreme sensitivity to alloy composition. This is especially true of active materials. Currently available simulation techniques can handle alloys with no more than two types of atoms. However, most real alloys contain four or more types of atoms. Thus, a new theory of composition effects in alloys is needed. I plan to use the mathematical theory of ``homogenization'' to develop a new methodology for predicting alloying effects. The goal of this theory is to predict the behavior of a ``composite,'' a complex material made up of several simpler materials. This is achieved by using only a knowledge of the behavior of the simple materials and a small amount of information about how these materials are combined, such as the relative amounts of each simple material contained in the final aggregate. Homogenization methods are commonly used with the traditional materials simulation techniques described in the Background section, but they have not been applied to the atomic level materials simulation techniques that are required to perform truly predictive materials design. Thus, I believe that homogenization methods, appropriately adapted for use with atomic level simulations, will represent a key technological breakthrough in the field of computational materials design.
Flaws in active materials and their effects on material properties: All materials contain flaws or ``imperfections.'' These include small holes, impurities such as atoms of a foreign material, or simply any irregular arrangement of atoms in the material that disrupts its natural highly organized crystalline structure. These imperfections are unavoidable and their presence can significantly affect the behavior of active materials. Imperfections exhibit complex interactions with a very large number of atoms within the material. Theoretical study of the interplay between imperfections and martensitic phase transformations has been largely unsuccessful and explicit atomic level simulation is a prohibitively time consuming task. To address the current lack of viable simulation techniques for the study of these problems I am working to develop a simulation method, based on the existing ``Quasicontinuum'' method for the pure elements (such as Si or Ni), that is capable of studying imperfections in complex alloys and intelligent materials. This method will be capable of rapidly and accurately studying the interaction between imperfections and the martensitic transformation in active materials.
Last Modified: 2019-06-28 at 08:24:30 -- this is in International Standard Date and Time Notation


