Austenite Twinned Martensite Microstructure
In a first order transition, both phases can coexist in a specimen
at the critical temperature 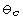 ,
and the austenite-martensite microstructure is the means by which the
transformation between the phases takes place. Typically, it is
observed that a homogeneous region of the austenite parent phase
coexists with a region containing parallel bands of alternating
layers of two variants of the martensite product phase. This latter
microstructure is a twinned martensite
microstructure. Macroscopically, the austenite twinned martensite
microstructure appears as depicted in Figure 1 below.
,
and the austenite-martensite microstructure is the means by which the
transformation between the phases takes place. Typically, it is
observed that a homogeneous region of the austenite parent phase
coexists with a region containing parallel bands of alternating
layers of two variants of the martensite product phase. This latter
microstructure is a twinned martensite
microstructure. Macroscopically, the austenite twinned martensite
microstructure appears as depicted in Figure 1 below.
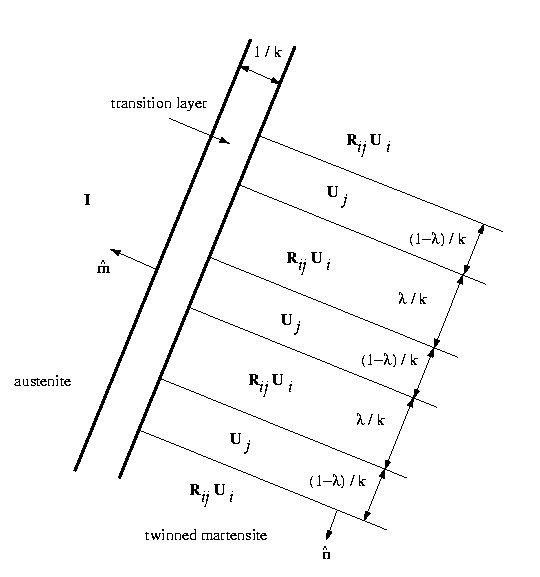
Figure 1: Austenite twinned martensite microstructure
In Figure 1, at the left is the austenite and at the right is the
twinned martensite. In order for the deformation to be continuous,
a transition layer is needed between the two phases. This layer
necessarily involves deformations with gradients not on the energy
wells; therefore, the microstructure is not an energy minimizer.
As noticed by Ball and James, however, if the width of the twins
and the width of the transition layer are both scaled by 1/k, then
in the limit as k goes to infinity, the deformation is continuous
and the gradient takes values solely from the energy wells.
With the variant pair (i:j), the compatibility equations for
the austenite twinned martensite microstructure are the twinning
equation
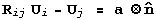
and a compatibility equation between austenite and a weighted
average of two twin related martensite variants, which can be
written as
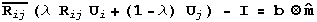
This equation is called the habit plane equation, and the unknowns
are the habit plane rotation 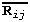 , the volume fraction of the twins
, the volume fraction of the twins 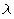 , the shape strain
, the shape strain
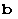 , and the habit
plane normal
, and the habit
plane normal 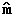 .
.
Solutions exist to the austenite twinned martensite microstructure
if and only if; a solution, vectors a and n, exist to
the twinning equation; and the conditions below are both satisfied:
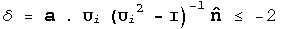 ,
,
and
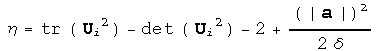 .
.
Here, Tr is the trace of the matrix, sum of the diagonal components, and
Det is the determinant of the matrix.
The first equation gives an eigenvalue equal to one, and the second
equation ensures that an eigenvalue is less than one and the remaining
eigenvalue is greater than one.
If the two conditions above are both satisfied, then the volume
fraction 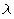 is given by
is given by
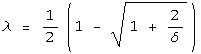 .
.
There are up to four solutions to the habit plane equation for
a given twin solution: two with volume fraction 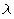 and two with volume
fraction 1-
and two with volume
fraction 1-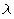 .
.
Symmetry amongst the variants and twin solutions can be used
to segregate any habit plane solutions into various sets of
symmetry related solutions. This is outlined
here.
Various austenite-twinned martensite microstructures are possible for
different transitions as listed in the table below.
In the table above, the first column is the transition; the
second lists the twin type for which solutions to the habit plane
equation are possible; the third column lists the number of unique
microstructures which can be formed; the last column gives some alloys
for which the various possible habits have been observed. This list
is by no means exhaustive.
(*) Note: for the cubic to monoclinic transition,
528 unique habit plane solutions are theoretically possible, while a
specific Ti-Ni alloy has only 192 habit plane solutions and of these
only 24 have been unambiguously observed in experiments.
Top of this page.
Back to main page.
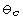 ,
and the austenite-martensite microstructure is the means by which the
transformation between the phases takes place. Typically, it is
observed that a homogeneous region of the austenite parent phase
coexists with a region containing parallel bands of alternating
layers of two variants of the martensite product phase. This latter
microstructure is a twinned martensite
microstructure. Macroscopically, the austenite twinned martensite
microstructure appears as depicted in Figure 1 below.
,
and the austenite-martensite microstructure is the means by which the
transformation between the phases takes place. Typically, it is
observed that a homogeneous region of the austenite parent phase
coexists with a region containing parallel bands of alternating
layers of two variants of the martensite product phase. This latter
microstructure is a twinned martensite
microstructure. Macroscopically, the austenite twinned martensite
microstructure appears as depicted in Figure 1 below.

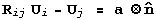
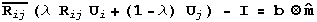
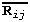 , the volume fraction of the twins
, the volume fraction of the twins 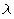 , the shape strain
, the shape strain
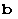 , and the habit
plane normal
, and the habit
plane normal 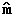 .
.
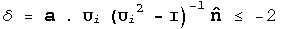 ,
,
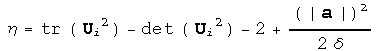 .
.
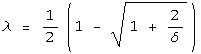 .
.
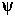 > 90 degrees)
> 90 degrees)