Highly Reversible Phase-transforming Materials
New phase transforming materials, even with strong first-order transformations, can be designed with low hysteresis and multimillion cycle reversibility.
Video of successive heating/cooling cycles in an alloy which has been tuned, by systematically changing composition, so as to satisfy the strongest known conditions of compatibility between phases.
Phase transforming materials have an abrupt change of crystal structure at the transformation temperature. This change can be quite drastic. So it can happen, for example, that one phase is a strong magnet and the other is non-magnetic. Such materials also are usually ferroelastic, meaning that they also change shape at the phase transformation. We call this "multiferroism by reversible phase transformation". Over the past 10 years we have been seeking the fundamental explanation of what causes some phase transforming materials to fail after a few transformation cycles, while others can go many millions of cycles. The Zn45Au30Cu45 alloy at left was discovered using a systematic theory-designed procedure. It is a big first-order phase transformation, exceedingly low hysteresis, and excellent reversibility. During heating and cooling it exhibits the delightful (and very unusual) non repeating microstructures shown. See [115], [116], [122], [141] and [161] for more details. We are collaborating closely with researchers from Kiel, Germany and Hong Kong in this work.
Origami structures
World population is growing approximately linearly at about 80 million per year. As time goes by, there is necessarily less space per person. Perhaps this is why the engineering community seems to be obsessed with folding things. Here is our approach.

A crease pattern and a few examples of the 65,534 ways this tessellation can be folded by varying only the mountain-valley assignments [157].
We depart from the standard approach to origami design which could be termed Eulerian -- develop relations between kinematic objects in the deformed sheet -- by developing a Lagrangian approach (describe the folding process as a deformation) [171]. We have previously developed a mathematical approach to ''rigid folding'' based on the use of piecewise rigid isometric mappings. A group orbit method using discrete isometry groups enables the design of complex structures from simple calculations. Our ideas are inspired by the way atomistic structures form naturally. These ideas are explained in our paper, ''Origami and Materials Science'' [157]. There are also fascinating mathematical analogs to the way microstructures form, as above.
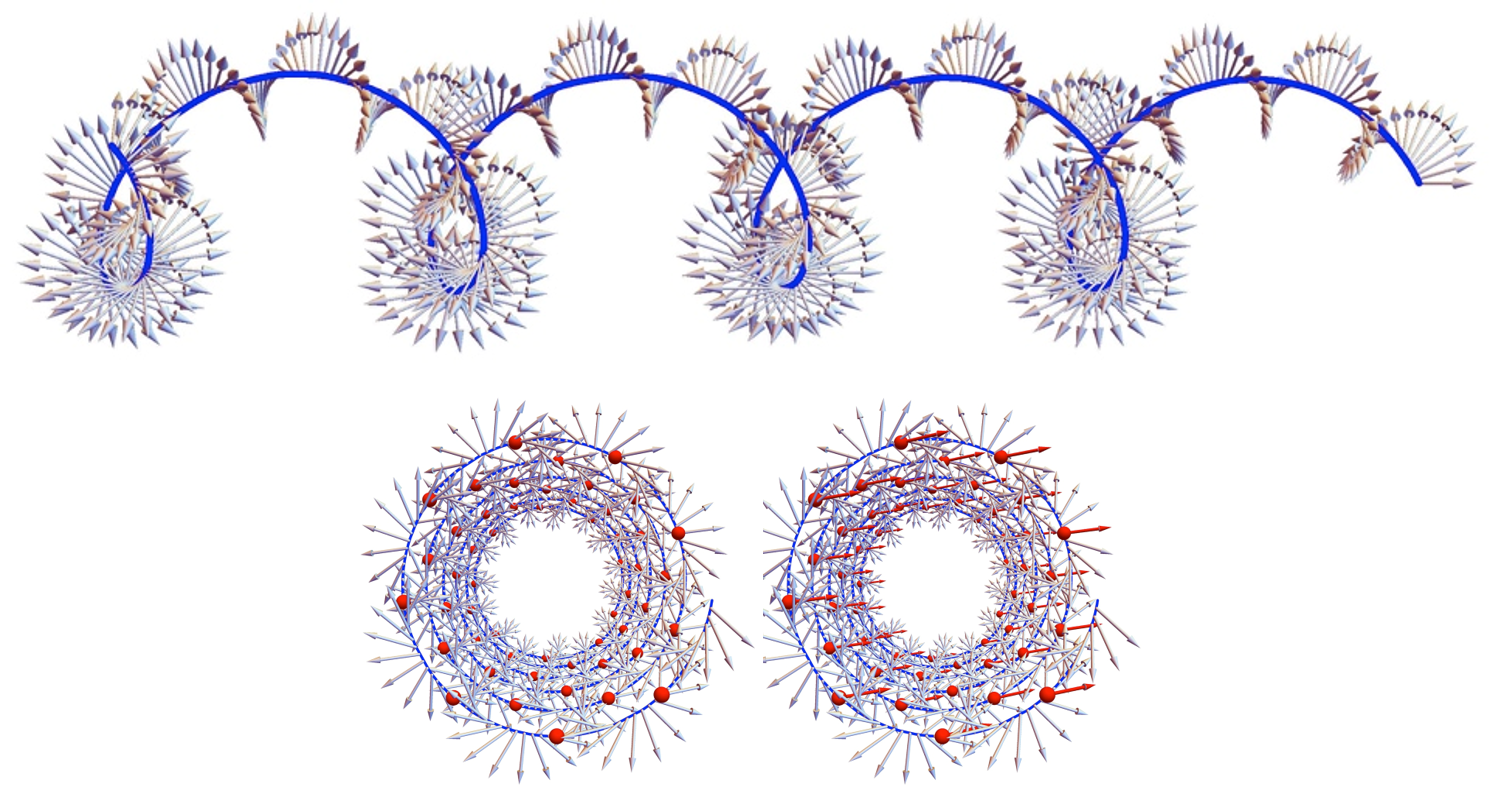
The folding motion of curved origami by introducing helical group.
The folding motion of curved origami by introducing circle group.
The folding motion of curved origami by introducing translation group.
Most recently, we depart from rigid folding by allowing the tiles to deform isometrically; that is, they are allowed to bend but not stretch. This is the way a piece of paper or sheet metal deforms. The work on curved origami structures with exact isometric deformations of the tiles is shown in the paper [178] and the videos on the right. Famously, buildings designed by Frank Gehry often use isometric deformations and some have creases: a great example is the Walt Disney Concert Hall. Our designs are like the Frank Gehry designs but are foldable from a flat sheet! The group orbit method also can be extended to the isometric case [169].
A revealing example of former postdoc Paul Plucinsky (Assistant Professor, USC) gives a simple 16x16 crease pattern that can be folded 65,434 distinct ways (above and [157]). And this is only the piecewise rigid foldings. If we allow curved creases and curved tiles, there is even more freedom. So, as one can imagine, the energy landscape of isometrically deformed origami structures can be exceedingly complicated. In the case that the energy is elastic energy due to deforming tiles, there is a wonderfully accurate theory to calculate the energy (and forces, moments) of these deformed tiles called Kirchhoff's plate theory. It says that the energy of a deformed tile goes as its thickness cubed. With different tiles having different thicknesses, there is tremendous latitude to design origami structures. We are trying to understand and manipulate this energy landscape to bias the structure to desired configurations, in a collaboration with the Air Force Research Laboratory. We also see relevance of some of these designs to the mitigation of climate change, but more about that to come. Currently, besides AFRL, we are collaborating with researchers at Caltech, Carnegie Mellon, Princeton, and Robert J. Lang.
Objective structures
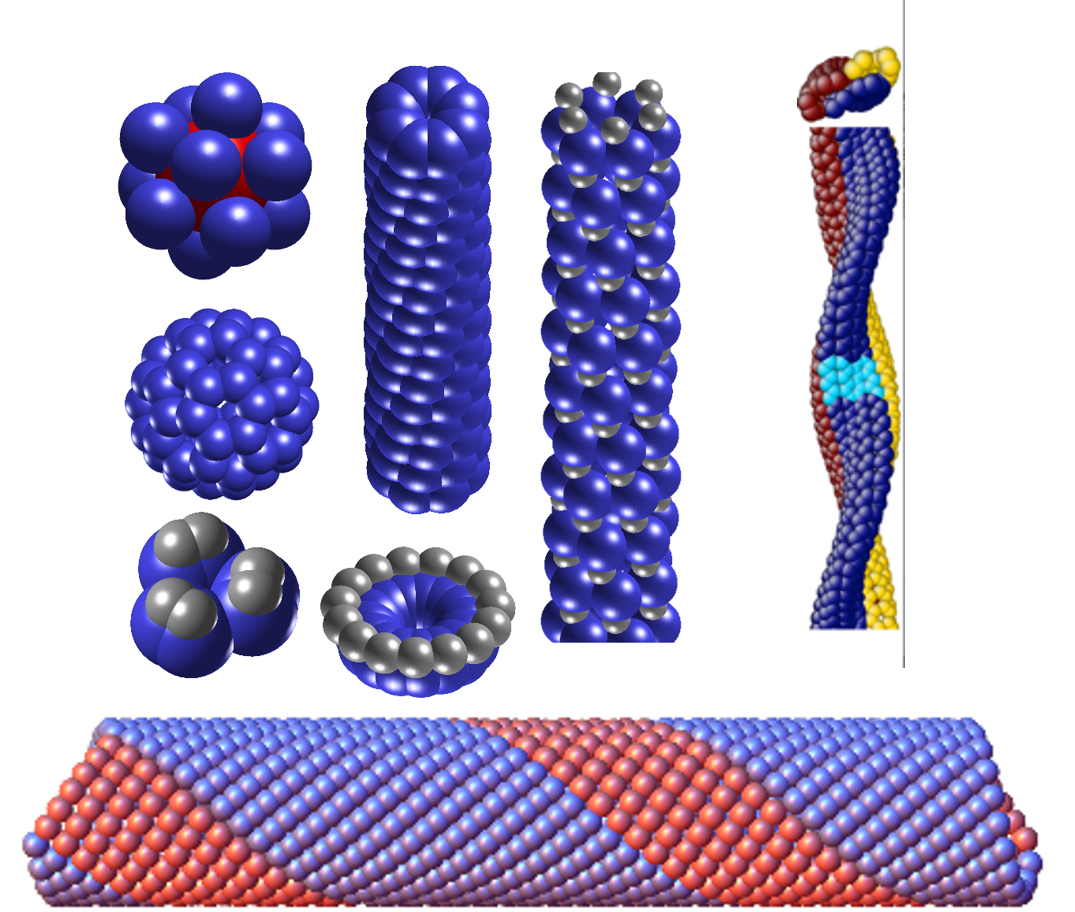
Graphene, carbon nanotubes, phosphorene and buckyballs have a peculiar structural feature that can be used in many ways for the discovery and analysis of new nanostructures.
In the simplest case "Objective structures" are atomic structures with the following property. Imagine a structure consisting of identical atoms. Now imagine sitting on an atom and looking around at your environment. Nearby, you see nearest neighbors, and, as you look further, you see more and more atoms of the structure. Now go to another atom of the structure. Objective structures have the defining property that, if you reorient yourself in just the right way, you see exactly the same environment. Briefly, atoms "see identical environments". There is a natural generalization of this idea to molecular structures. What is so surprising is that many of the most intensely studied nanostructures today - graphene, single-walled carbon nanotubes of any chirality, phosphorene, buckyballs, many viral structures - have this property.
In fact there is something much deeper going on. The whole subject is much more about invariance than structure [140]. The classical equations of physics -- including also quite general versions of nonrelativistic quantum mechanics -- have invariance groups. These are groups of transformations that take a solution into a solution. A familiar group of this type is the Galilean group: orthogonal transformations and time-dependent translations with affine time dependence. It turns out that all objective structures can be generated by applying these groups to a collection of atoms. ''Applying'' means there is a rule for doing this, and there is also simple rule (called the group product) for how to multiply two Galilean transformations. But there is an added feature: due to the time dependence, the objective structures deform in time.
A simulation that employs Lennard-Jones argon, ultimately yielding a macroscopic motion with extension and shear. The initial state depicts the simulated atoms (blue). The nonsimulated atoms (red) fill the entire space, but for clarity, only those in the parallelepiped are shown; this parallelepiped is deformed from the cube according to the macroscopic motion. The larger simulated atoms are closer to the reader. Note that the simulated atoms quickly diffuse into the sea of nonsimulated atoms.
So, here is the game, in the case of molecular dynamics. Take any number of atoms (the ''simulated atoms'') and put them anywhere. Start them with any initial velocities. At every time-step apply the Galilean group to these atoms to get the nonsimulated atoms. Solve the equations of molecular dynamics for the simulated atoms only, accounting for the fact that the some nonsimulated atoms may be close enough to a simulated atom that we must account for the force it exerts. Now the remarkable fact: even though the simulated atoms behave highly chaotically, and quickly diffuse into the nonsimulated atoms, all atoms, simulated and nonsimulated, satisfy exactly the equations of molecular dynamics (MD) for their forces. More than that, all accepted models of continuum mechanics -- Navier-Stokes equations, nonlinear elasticity, and more complex materials -- have exact solutions for all values of the material constants that are the exact averages of these MD solutions. See [172] and [175] for more details.
We are using this property in many ways, from the design of new fast methods of doing molecular dynamics to new methods for accurate first principles calculations. In this work, we are collaborating with a broad collection of researchers from Berkeley, Caltech, Carnegie Mellon, Cornell, Georgia Tech, Lawrence Berkeley Laboratory, TU Munich, UCSB, UMN and Rome.
Energy conversion
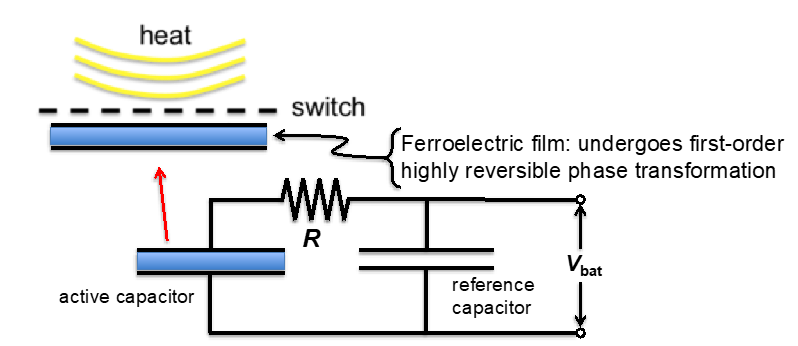
Phase transforming materials can be made to have one phase that is a strong magnet and the other phase nonmagnetic, or, one phase is a strong ferroelectric and the other non ferroelectric. We call this "multiferroism by reversible phase transformation". Such materials can be used for the direct conversion of heat to electricity.
We show how a new multiferroic material they created begins as a non-magnetic material then suddenly becomes strongly magnetic as the piece of copper below is heated a small amount. When this happens, it jumps over to a permanent magnet. This demonstration represents the direct conversion of heat to kinetic energy.
The concept of "multferroism by reversible phase transformation" can be used in many ways, and we are particularly exploring its possible application to direct energy conversion. In this context "direct" means that the material itself generates the electricity, without a separate electrical generator. We started by using a NiCoMnSn alloy (discovered in our lab) for which the high temperature phase is strongly magnetic an the low temperature phase is nonmagnetic. Passing through the phase transformation by heating, one can convert the abruptly changing magnetization into electricity, by induction. We studied this theoretically and realized it has some disadvantages: good properties for induction conflict with good heat transfer. Guided again by theory, and with Prof. Bharat Jalan, we are now working on the case of an abrupt ferroelectric transformation, which is proving to be extremely promising, see [144] and [147]. Generally, these methods are good for the "small temperature difference regime", e.g., solar-thermal sources, waste heat from air conditioners, data centers, exhaust systems, or even hand-held electronic devices, for which there currently exists no reasonable method of energy conversion.
Interaction of radiation and objective structures
Almost everything we know about the structure of matter comes from X-ray methods. To implement them, one needs a crystal. But what if the material is impossible to crystallize, or, say, prefers a helical structure rather than a periodic one?
Almost everything we know about the structure of matter, whether materials science or biology, comes from X-ray methods. (We are trying to change this situation - see above - but the theoretical methods are not yet accurate enough to compete with X-ray methods.) How do they work? One shines plane waves at X-ray wavelength on a crystal, and by changing the relative orientation of plane wave and crystal, one gets constructive interference, that is, strong spots on the detector. Tune the wavelength slightly, and suddenly one gets strong destructive interference. The mathematical reasons for this behavior comprise a fascinating chapter in Fourier analysis, with a digression into number theory and the invariance of differential equations. Could one do that same thing for other "regular" structures such as objective structures. With Prof. Gero Friesecke and his group at TU Munich, we are investigating this possibility [132]. Some of the new solutions of Maxwell's equations that interact constructively with objective structures also have other unexpected properties such as orbital angular momentum, and interact with materials in unusual ways.
Magnetic hysteresis
Hysteresis is synonomous with loss, and thus is usually unwanted in a vast array of applications. We learned a lot about hysteresis in phase transformations, which is primarily related to the fitting together of the phases. Magnetic hysteresis is different, but can we borrow some of the modes of thought to understand the origins of magnetic hysteresis in a predictive way?
Hysteresis in phase transformations refers to the property of transforming at a higher temperature on heating than on cooling. Similarly, in stress-induced phase transformation, beginning in one phase, the transformation stress with increasing stress is higher than that of the reverse transformation.
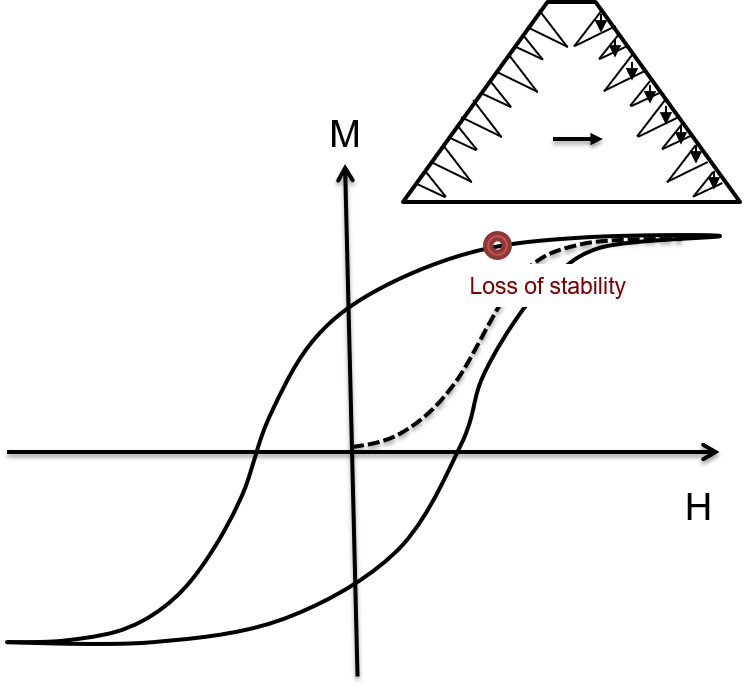
Although there remain significant questions in the case of stress-induced transformation, we learned a lot about the fundamental origins of hysteresis in phase transformations [141]. Using these ideas we now routinely make alloys with big first order phase transformations and thermal hysteresis of 2-3 C. Mathematically, hysteresis in phase transformations concerns primarily the fitting together of phases, and the energy barrier that results when they do not fit together so well. With groups at Colorado School of Mines and Case, and the postdoctoral work of Ananya Renuka Balakrishna (Assistant Professor, UCSB) we decided to tackle magnetic hysteresis, particularly in soft magnetic materials. We believe there may be a similar energy barrier, but not due to fitting and decidedly more subtle in this case. The fundamental mathematical challenge here is that this barrier -- also in the case of phase transformations -- is not discovered by doing a linear stability analysis of the state that is just about to transform. That was tried extensively in the 1950s-1970s and its failure goes by the name of the ''coercivity paradox''.
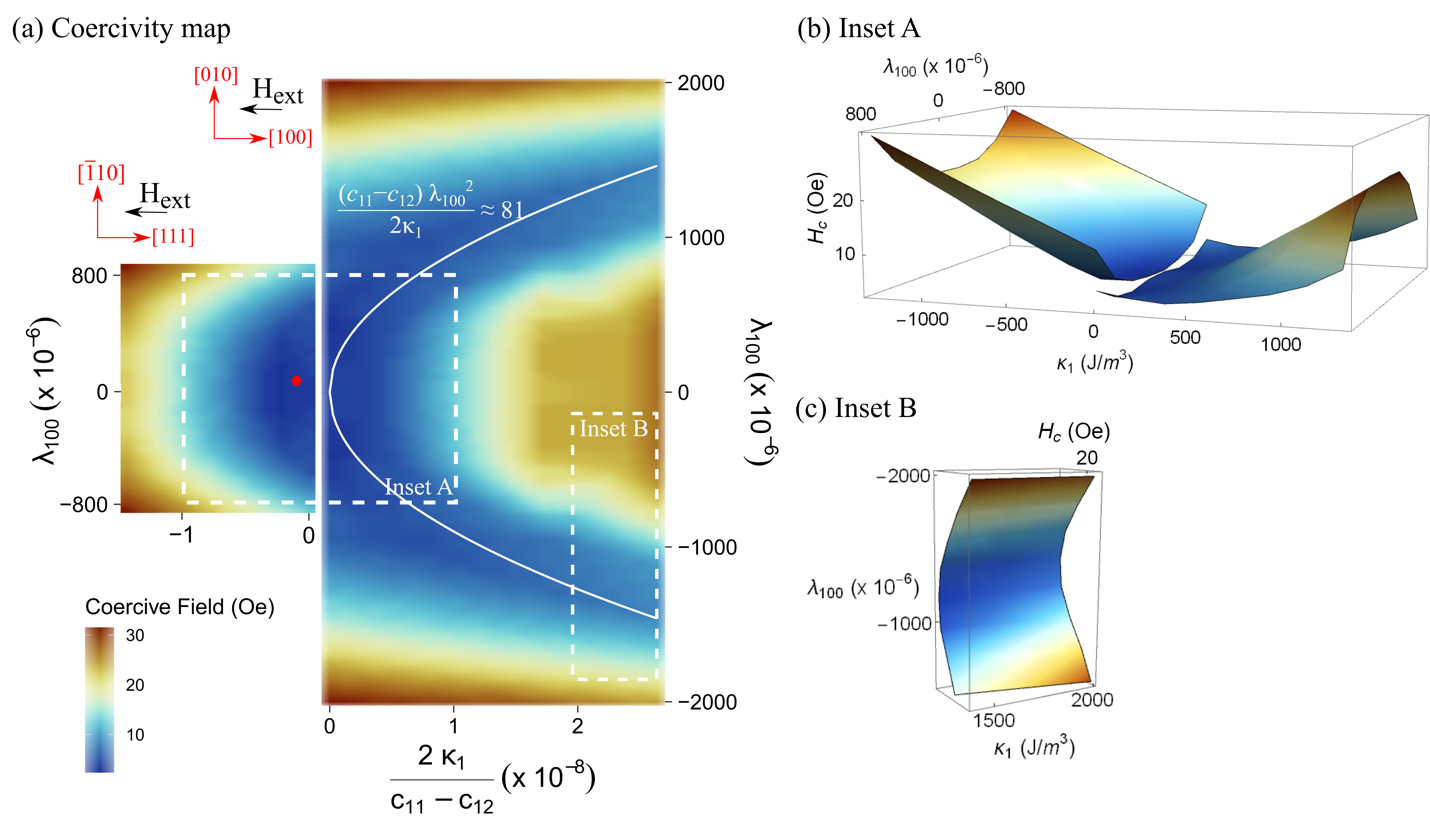
Color map of coercivity (half width of the magnetic hysteresis loop) as a function of the magnetostriction constant Lamda100 and dimensionless anisotropy constant 2*K1/(c11-c12). The red dot is the famous low hysteresis alloy permalloy. Materials with large K1 are predicted to have low hysteresis as long as the magnetostriction constant is tuned suitably [167].
From the work on phase transformations we had an idea that magnetostriction may be important, even though it tends to be quite small in the magnetic materials. Ananya Balakrishna developed a sophisticated multiscale micromagnetic code, with an optimized defect, that circumvented the coercivity paradox [167]. As a rule of thumb, it is universally believed that to make a low hysteresis magnet, one needs either to make a nanocrystalline material, or make a certain constant (the anisotropy constant) vanishingly small. Contrary to conventional wisdom, she predicts with a high degree of confidence that materials with large anisotropy constant will have very small hysteresis as long as the magnetostriction constants are tuned to special values. We really like results like these: simple, precise and completely unexpected.
See the home page for our current research projects. Prospective graduate students and postdoctoral fellows with interests in any of these areas are encouraged to contact Prof. James for more information about openings.